To DOWNLOAD CAMEROON GCE JUNE 2011 math meach Paper 2 click on the link below
June 2011
1. The position vector r of a particle at time t seconds is given by r = [(acoswt)i + (bsinwt)j]m, where a,
b, and w are constants and i and j are unit vectors in x-direction and y-direction respectively.
(a) Find the magnitude of the velocity of the particle when t=0
(b) Find the angle between the position vector and the acceleration vector of the particle at any time
(c) Show that the acceleration of the particle is always directed towards the origin of the coordinate
axes.
(d) Obtain the Cartesian equation of the path of the particle
2.
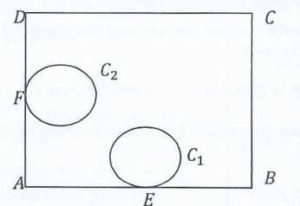
Figure 1 is a uniform square lamina ABCD, of side 6a. C1 and C2 are circular portions of the lamina, each of radius a. The side AB of the lamina is tangent to C1 at its midpoint E, while the side AD is tangent to C2 with its midpoint F. The portions C1 and C2 are removed from the lamina.
Find the distance from DC and from BC of the centroid of the remainder of the lamina. Hence, show that if the angle of inclination of BC to the vertical when the remainder of the lamina is suspended freely from C, then tan θ = 1.
3. Two particles of mass 25kg and 35kg are attached to the end a light inextensible string which passes overthree smooth pegs P, Q and Rina wall arranged in the form of an isosceles triangle with angle QPR = 90°, the side QR horizontal and below the peg P.
The system is released from rest with the string taut. Find,
(a) The acceleration of the system,
(b) The tension in portion of the string,
(c) The reactions on pegs P and R.
4. (i) A car of mass 2200Kg tows a carriage of mass 800Kg from rest, along a straight horizontal road. The
total resistance to the motion of the car 200N and the resistance to the motion of the car is 200 N and the resistance to the motion of the carriage is 100N. Given that the tractive force of the engine of the car is 600N, find,
(a) the acceleration of the system,
(b) the tension in the rope,
(c) the speed of the system at a distance of 2000 m from the starting point.
(ii) An inelastic string of length 150 cm is fixed at a point A on a ceiling. The other end B carries a particle of mass 6 kg. The particle describes horizontal circles of radius 90 cm below A. Find the speed of the particle and the tension in the string.
5. (i) A uniform see-saw beam AB of mass 20 kg and length 10 metres is pivoted at a point 0.6 metres from
A. A boy of mass 70 kg sits 4 metres away from A. Find how far from B a boy of mass 100 Kg must sit, for
the system to be in equilibrium.
(ii) One end A of a uniform ladder AB of length 2a and weight W, rest against a rough wall, and the other end B against a rough horizontal ground.
The coefficients of friction at the wall and ground are µ1 and µ 2 respectively.
Find, in terms of µ1 and µ 2 ,
(a) The tangent of the angle which the ladder makes with the horizontal ground when it is at the
point of slipping.
(b) The magnitudes of the normal reactions at the wall and the ground.
6. (i) A Horizontal force of magnitude 50 N pushes a particle of mass 50 Kg up a rough plane inclined at an angle θ to the horizontal, where 5 sin θ = 3. The particle starts from rest at P and moves along the line of greatest slope, reaching A point Q distance 12 metres from P.
Given that the coefficient of friction between the particle and the plane is 1/3 calculate
(a) The velocity of the particle at Q,
(b) The time taken by the particle to reach Q.
(ii) A force of magnitude 5 N stretches a string by 0.3 m. Given that the modulus of elasticity of the string is 10 N, find.
(c) The natural length of the string,
(d) The work done in extending the string by 0.3 m from its natural length.
{Take g as 10ms-2)
7. Three smooth spheres A, B and C of equal radius and mass 2m, 7m and 14m respectively, lie at rest in
a straight line on a smooth horizontal floor, with B between A and C.
The coefficient of restitution between each pair of sphere is ½ .Sphere A is projected with speed u to collide directly with sphere B which subsequently collide directly with sphere C.
(a) Show that B comes to rest after its collision with C.
(b) Find the total kinetic energy of the system immediately after B collides with C.
8. In a centre for handicapped people, there are 100 women and 240 men. It is known that 15% of the women and 30% of the men suffer from leprosy. A handicapped person X is selected at random from the centre. Draw a tree diagram to illustrate all the possible outcomes. Hence, or otherwise, find the probability that
(a) X is suffering from leprosy,
(b) X is a man given that X is suffering from leprosy,
(c) X is a woman or X is suffering from leprosy,
(d) X is a woman given that X is not suffering from leprosy,
(e) Show that the events
A: X is a woman and
B: X is suffering from leprosy,
Are not independent.


















Elmerex latty
May 31, 2021
I'm very happy that I could download this paper, because this app doesn't work on my present phone and it worked on my previous phone. It is a wonderful I app I wished to have in my phone, but it doesn't match with my OS or whatever was the problem, this has really been helpful and ai advice you guys to try out the app, its cool