Young’s Modulus and Determination of Young’s Modulus

In  this article we will going to introducing, what  is Young’s Modules and how it is determined using the Beam method. This article is under our Matter series. This topic is often seen in the gce, gcse and the gce A level.

 

Elasticity

 

Basic Definitions

Consider the graph below

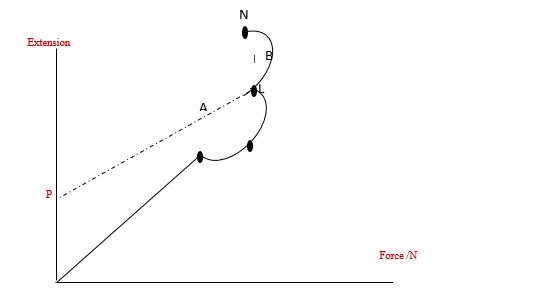
Where on equals the elastic limit.

• AL is nonlinear but plastic.
• L deformation is plastic, does not own to its original shape or length.
• PB Permanently stretched so if loaded follows the curve PB
• N Breaking point or where the material is almost about to break.

Tensile Stress: This is the force per unit area where the area A is per perpendicular to the force N

i.e tensile stress = Force/Area,  I.S Unit for stress = Nm-2 or Pascal Pa

Tensile Strain : This is the ratio of the extension e to the original length L₀ of the material.

i.e  tensile strain = extension/original length, I.S Unit = it has no unit

 

Young Modulus (E) : This is the ratio of the tensile strain to the tensile stress

i.e.   E= tensile stress/ tensile strain.

S.I unit Nm-2 or Pa

 

E = T.stress/T.strain

= (Force/Area) / (E/L0)

= (Force/Area) x (L0/E)

E = FL0/Ae.

 

Dimensions = ML-1T-2.

Note

T.stress = tension/cross-sectional area.

A =π²d/4 (cross sectional area)

E= 4FLo/πd²E                    d=2r, r=d/2

 

Exercise

An Al wire of length 0.35m and radius 0.20mm is stretched by 1.4mm young’s modulus of Al is 7.0 * 10pa

• Fine the strain in the wire.
• Fine the stress in the wire.
• Find the cross sectional area in the wire.
• Find the tension on the wire.

(Solution at the bottom)

 

Determination of Young’s Modulus

 

 

 

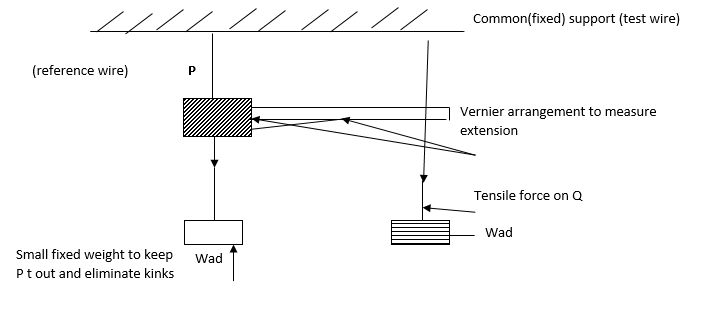
1. P and Q are wire of the same material, same length and dimension
2. The wires are thin, long to ensure that material loads produce extensions that are measurable.
3. The areas are free from kinds (Not twist) so that the extension will be that of the wire and not of the kink.
4. This is done by hanging loads at this ends.
5. The dimension of the wire is also measured using a micro meter screw gauge at several places and the average is gotten
6. The cross-section area A is measured A=πd²/4 in m
7. The wire Q is loaded readings noted such terms with the corres ponding load. The load is removed in steps of 1kg. If the readings of the vernier are very nearly the same when the wad was exceeded.
8. The reading of the force (load) and extension are recorded on a table as shown below.

Force/ N
Extension / M
Stress / Pa
Strain
Young’s Modulus

 

Calculation of D

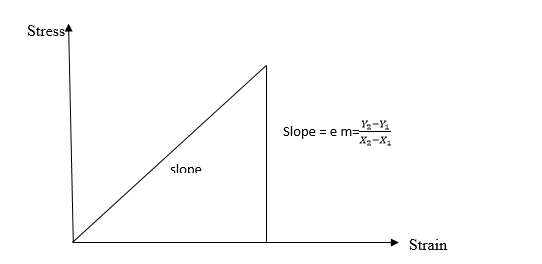
A graph of stress against strain is plotted. It is a straight line passing through the origin as shown below. The gradient or slop gives E (Young’s modulus).

 

OR

A graph of force against extension can also be plotted. It is a straight line passing through the origin as shown below.

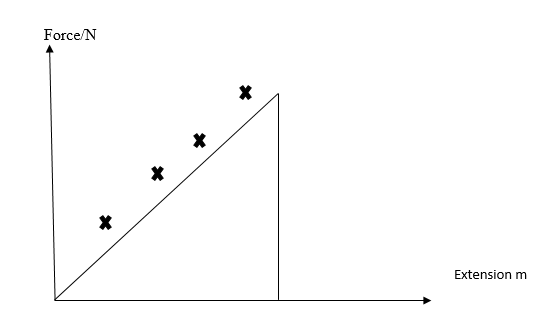
From E = EL0/Ae

Gradient =F/e  is found from the graph knowing lo, A and E

Can be calculated using the above formula.