To DOWNLOAD CAMEROON GCE JUNE 2010 math meach Paper 2 click on the link below
JUNE 2010
1. The position vector r, of a particle P, of mass 2Kg at time t seconds, is given by r = [(t3 – 2t)i + t2j]m.
(a) the values of P for which the velocity of P is perpendicular to its acceleration,
(b) The force acting on P and the momentum when t = 3,
(c) The cosine of the angle between the force acting on P and the momentum of P when t = 3.
2. Figure 1
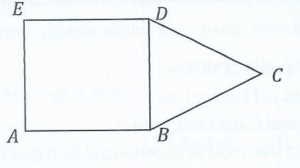
Figure 1 is a uniform density lamina ABCDE, made from a square of side 2a and equilateral triangle of side 2a. Show that the distance of the centriod of lamina from BD is
(3a(4- √3))/13
The lamina is freely suspended at E so that it rests in equilibrium with ED inclined at an angle 6 to the
vertical. Show that
tan θ = (14-3√3)/13
3. i) A block of mass 5kg lies at rest on a rough horizontal plane. The coefficient of friction between the block and the plane is 0.6. A force of magnitude 20N is applies to the block at an angle of 300 to the horizontal. Find the frictional force between the block and the plane. Investigate whether the block has been set in motion by this force.

Forces of 10N, 8N and 6N act along the sides BC, CA and AB of an equilateral triangle ABC as in figure 2. Find the magnitude of the resultant of these forces and the angle which it makes with BC.
A golf player project a ball from a point on horizontal ground with a speed of 50MS_1 inclined at an angle to the horizontal. The ball passes through a point P which is at a horizontal distance of 200m from the point of projection and at a vertical distance of 25m above the point of projection. Find the possible values of tan θ.
For the smaller value of tan θ, find the magnitude of the velocity of the ball at P and the range of the ball on the horizontal plane through the point of projection.
(Take g as 10ms~2)
A car of mass 1500kg tows a carriage of mass 500kg. the frictional resistance to the motion of the car is 700N and the frictional resistance to the motion of the carriage is 300N. The engine of the car works at a
constant rate of 20KW. Find the acceleration the car and carriage and the tension in the rope when the speed of the car is 5ms-1.
On level ground,
Directly up a track inclined at an angle 6 to the horizontal, where sin θ=1/20
(Take g as 10ms~2)
Three sphere A, B and C of equal radii have masses m, 2m respectively. They lie in a straight line on a smooth horizontal plane with B between A and C. The coefficient of restitution between any pair of
spheres is A is 1/3 projected with speed u to collide directly with B. Show that the speed of B after impact 4u/9 is and find the speed of A after impact B subsequently collides with C. Find
The speeds of B and C after this impact,
The magnitude of the impulse experienced by B due to the impact,
The loss in kinetic energy due to the impact between B and C.
A particle of mass 4kg moves in a straight line under the action of a force of magnitude
(16- v2)N, where v ms2 is the speed of the particle. Initially the particle is at rest at the origin.
Show that the speed of the particle at time t seconds can be express as v =4(e^2t-1)/((e^2t+1))
and deduce that the particle cannot attain a speed of up to 4ms-1.
i) Two event A and B are such that P(A) = 2/5 and (A U B) = 7/10. Find P(B) if
A and B are mutually exclusive.
A and B are independent,
P(A\B) = P(B\A)
ii) A box contains 4 red balls and 6 yellow balls. A ball is drown at random from the box, its colour is noted and it is returned into the box together with another ball of the same colour. A second ball is drawn from the box.
Draw a tree diagram illustrating the possible outcomes. Hence, or otherwise, find the probability that
Two red balls are drawn.
Two balls of the same colour are drawn
At least one yellow ball is drawn.


















